Finding the Fun in Math at Home
Editor’s note: Hi folks, meet Heather Moore, who I’ve been collaborating with on Pixidoku puzzles. Heather is a math teacher and has some great tips to offer for those of you who are looking for at-home learning activities for your kids. Take it away, Heather! — Jim
In the midst of a global crisis, I’ve been noticing some silver linings and surprising upsides. This is not to downplay the seriousness of it all or dismiss any of the real loss and suffering in our world, but I feel it is important to take hold of the good things that can be found amidst all the uncertainty and struggle.
Being stuck at home can be seen as a chance to spend more time with family. Being unable to do some kinds of work can free up time for projects that otherwise get neglected. And a break from math class can be an opportunity to play with math together.
I know, I know. The words “play” and “math” in the same sentence? Hear me out. In my world of teaching math to homeschoolers I find that the more playful I can make math, the better. So today I want to share with you a couple ways I’ve been playing with math with my students this week.
The 11’s Game
Quick! What’s 11 x 7? If that was easy for you, it is probably because you know the rule for this pattern: 11, 22, 33, 44, 55,… Just repeat the digit you’re multiplying by. This is cool by itself, especially for younger learners, but it gets better!
I introduce the 11’s game by showing off a little for my students. They have calculators in hand to check me. I tell them, “Give me any two-digit number and I will multiply it by 11 in my head.” “43!” Someone calls out. “473” I respond immediately. “52”, “572!” and the inevitable “99” “1089!”
Once they are impressed, or at least intrigued, I inform them that with the use of a simple pattern they can learn to play the 11’s game just as fast as I can.
Check out the following multiples of 11. What do you notice?
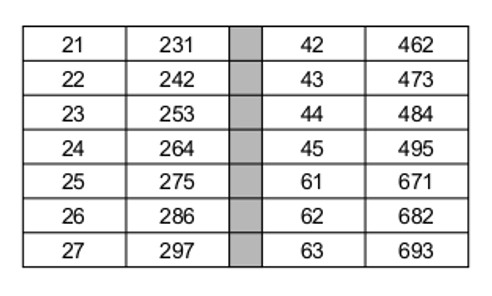
The pattern is easier to see than it is to describe, but here’s one way to put it: Take the digits of the multiplier and add them together. Put the resulting digit in between the two original digits to create your three digit product. So for 63 x 11 you add 6 + 3 to get 9 and nestle the 9 in between the 6 and the 3 to get 693.
Always start off practicing examples where the sum of the two digits of your multiplier is less than 10. Then see if you can expand the rule to allow you to deal with cases where the sum is greater than 10.
All of my tutoring that is usually done in person has had to move online for now. I find the change exhausting, but pulling this game out with one of my students had him literally shrieking with amazement and delight, giving our online tutoring session a much needed energy boost.
After enjoying the game in a purely playful spirit, I test the waters for some deeper mathematical exploration. Some students will be intrigued enough by this trick that they will want to figure out why it works. I try my best not to explain, but to instead encourage them to make sense of it for themselves. It doesn’t need to happen all at once, and patience here is rewarded with the pure delight of genuine mathematical discovery.
The Game of Nim, or “Last Pebble”
The week after the schools in my area shut down, my family went out camping on family property for a week to get away from populated areas. Even though I had my small dry erase boards with me and a Life of Fred math book, one of my favorite math games didn’t require any of those things.
One of the girls and I set about preparing for the game: We collected about 20 smallish pebbles and found a flat log to use as a playing surface. When I’m in the classroom I use base 10 block unit cubes, but you can use coins, poker chips, dried beans or any other kind of small counter or token.
The American mathematician Charles L. Bouton named the game ‘Nim’ in 1901, but it is an ancient game, no doubt played under many names, and I like to call it “Last Pebble”, “Last Coin”, or “Last Cube” depending on what we’re playing with.
To play, arrange your “pebbles” in three piles. One player gets to set up the piles, choosing the number in each starting pile, and the other player gets to decide who goes first. Players take turns removing some number of pebbles from one of the piles. You are allowed to take an entire pile if you like. You must take at least one pebble on your turn and you may not take pebbles from more than one pile on your turn. The player to take the last pebble wins.
When I’m playing with a new player I start off by trying to win about half the time. If I’m able to win by taking the final pile, I always do so, but I often will make deliberate bad moves earlier in the game to give my new opponent opportunities to beat me.
Once a new player has caught on to some of the basic strategy, I offer “puzzle mode”. We play once, with both of us trying our best to win. Having worked out quite a bit of the ideal strategy, I usually win. When I do, I will have noticed an interesting position late in the game that could be used as an instructive puzzle. Usually it’s either a game state where I knew for sure I was going to win, or where I noticed they could have won with a different move than the one they made. We return to this game state repeatedly, with the new player choosing whether to go first or second each time we replay it, until they can beat me at the puzzle.
A basic puzzle set up to try is three counters in the first pile, three in the second, and zero in the third. Again, reset the puzzle each time the player loses and have them choose again whether to go first or second. Here are some other good puzzles I use: (2, 2, 4) (1, 2, 3) (1, 3, 5).
For a deeper challenge, my students and I will try to map out ideal strategies for each player and get to the point where we can look at any starting board and be able to tell if the first or second player will ultimately win, given perfect play from both players.
Thank you for for reading. I hope you find these ideas useful and that they help bring a little mathematical silver lining into your world.
(More from Heather at monkeyflowermath.com)