Sudoku Troubleshooter #2 – XY-Wing
This is part of a series on puzzle solving techniques. If you are stuck on a particular Krazydad puzzle, drop me a note, and I’ll use this space to help you out.
This puzzle is also from Margaret, who got stuck on a Tough puzzle (Tough #4 from book 40). If you’d like to try your hand at this puzzle, you’ll find the original here.
Here’s the puzzle at the point where Margaret got stuck.
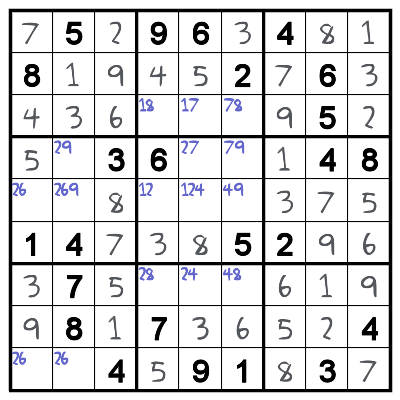
It looks nearly done, but the remaining cells look nearly intractable. Normally, I’d be tempted to just substitute in a value and see what happens, but there is a more logical way to approach it. It turns out there is an XY-wing lurking in there. You can read about the XY-wing technique here.
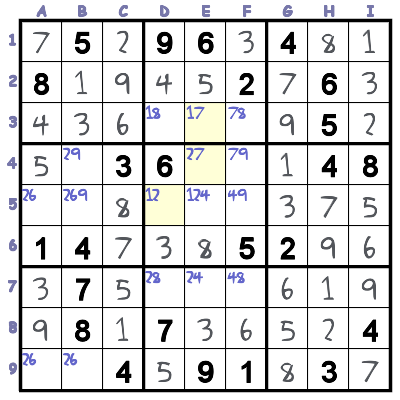
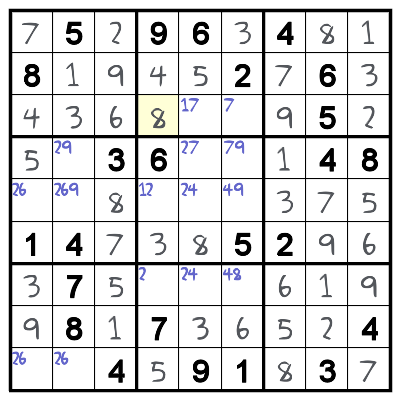
The root of the XY-wing is cell E4, which has 2 and 7 as possibilities. It is connected to cell E3 (which can be 1 or 7) and cell D5 (which can be 1 or 2). Think about the ramifications: If E4 is 2, then D5 must be 1. If E4 is 7, then E3 must be 1. Since E4 can only be 2 or 7, either E4 or D5 must be 1. This means that any cell that is simultaneously connected to both E4 and D5 cannot ever be 1 (because it would prevent both E4 and D5 from being 1).
This means we can clear 1 as a possibility from cells D3, and E5.
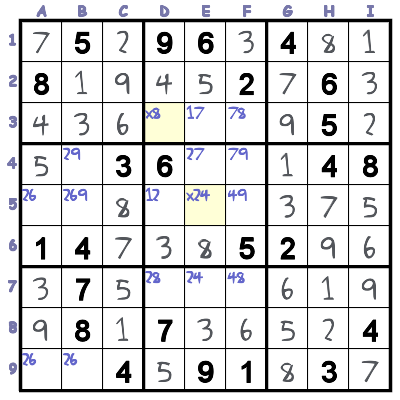
Both of these cells are connected to both E4 and D5. Once we’ve cleared the 1s out, it’s obvious that D3 must be 8. Now the rest of the puzzle solves easily.
As it turns out, XY-Wing crops up pretty frequently in the Tough puzzles. In book 40 alone, puzzles 2,3 and 4 make use of it.
UPDATE: Stephen wrote me with an alternate breakthrough which makes use of the knowledge that the puzzle must have only one solution:
My wife Stella had an insight…
Looking at column B, assume B4 is a 9, then A5, A9, B5 and B9 all have the same possibilities and there would be two possible solutions; ergo B4 is not a 9 but a 2 and away you go.
Of course this is contingent upon there only being one possible solution…
Pretty clever!