Rhombille Slitherlinks
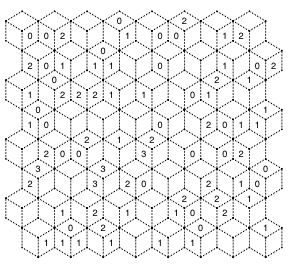 Fans of my variety slitherlinks will enjoy these two new sets of puzzles, based on two different Rhombille tilings supplied by reader Lars Huttar.
Fans of my variety slitherlinks will enjoy these two new sets of puzzles, based on two different Rhombille tilings supplied by reader Lars Huttar.
The first set (shown here) is a basic rhombille tiling with intersections containing 3 and 6 vertices.
The second set contains intersections of 3, 4 and 5 vertices.
Rhombille Set #1 (six puzzles)
Rhombille Set #2 (six puzzles)
UPDATE: Here’s a full set of these puzzles, using the second tiling..

January 13th, 2011 at 6:21 pm
I’m looking forward to these! Incidentally, the link to your ‘variety slitherlinks’ just seems to come back to the blog page. And I’m getting a 404 for the Rhombille Set #2.
January 13th, 2011 at 7:18 pm
Fixed – thanks for catching those Blaine!
January 13th, 2011 at 9:12 pm
For those who are interested…
I was interested in seeing Slitherlink puzzles on a Rhombille tiling because I like the 3D feel of this pattern. On all the variety slitherlinks, I enjoy watching the path emerge, and especially the shape of the region contained by the path. I thought it would be fun to watch the path and the contained region going up and around the 3D cubes.
In the 2nd set of puzzles linked to here, I did two things to boost the 3D effect of the Rhombille pattern. One was to make some of the cubes “sink into the page” instead of all of them “poking out.” In terms of the graph, some of the vertices with three edges are connected to the nodes directly above, to the southeast, and to the southwest, instead of to the nodes below, and to the northwest and northeast. As Jim mentioned, this has the effect of causing the vertices at the edges of the cubes to have 3, 4, 5, or 6 edges, instead of just 3 or 6.
The other thing was to skew the “cubes” a bit so that the front top vertex and the bottom rear vertex are not aligned with each other from the viewer’s perspective. This makes the “sunk in” and “poking out” cubes easier to distinguish visually. I think it’s what is called an oblique projection, and is similar to a cabinet projection. This doesn’t affect the topology of the puzzle at all — it’s just a cosmetic change. But my motivation was aesthetic. :-)
So, hope you enjoy these. Thanks, Jim, for posting them.