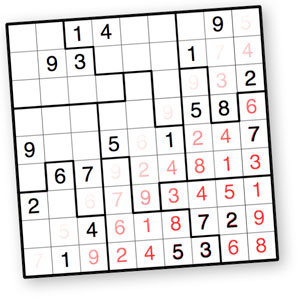I recently added a new puzzle variety to Krazydad, called Jigsaw Sudokus. These are very similar to normal Sudokus. Like those puzzles, each row and column contain all the digits 1 through 9. However, these puzzles are missing the 3×3 blocks found in regular Sudoku. Instead, the puzzles are divided into a set of irregular “jigsaw” pieces – each of which also contains the digits 1 through 9.

In my collection, the Jigsaw layouts are always different, so each puzzle offers a unique challenge which you won’t find in regular Sudoku.

Because these puzzles are a little different, I thought I’d offer a short tutorial to help you get started. I’ll start by solving just a couple squares of Puzzle #3 from book 1 of the Tough puzzles.

In particular, I want to demonstrate the one unique strategy that these puzzles require, apart from the regular Sudoku strategy you already know. This is called the “Law of Leftovers”, or the “Rule of Overlaps”. Take a look at the puzzle, below.

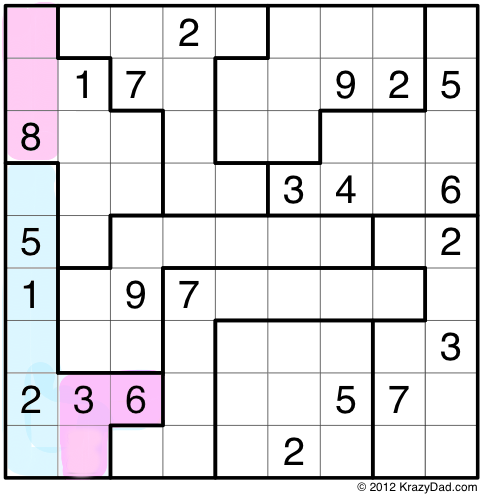
You’ll see that I’m interested in the jigsaw piece on the lower left, which I’ve colored mostly in blue. When you compare this piece to the first column, you’ll see that 3 cells stick out on the bottom (they contain a 3, a 6, and blank). I call these cells “outies”. There are also three cells left over at the top of the column (“innies”), which contain two blanks, and an 8. I’ve colored both sets of cells pink.

What may, or may not be obvious to you, is that the innies and the outies must contain the same set of 3 numbers. Why? The jigsaw piece must contain the numbers 1-9. The first column must also contain the numbers 1-9. The 3 outies must contain all the numbers from 1-9 which don’t appear in blue, and the 3 innies must also contain the numbers from 1-9 which don’t appear in blue. These three numbers must be the same, in both cases.

Since the innies contain an 8, the outies must also contain an 8. Since the outies have only one blank, and no other 8s, the blank on the bottom must be the 8. Similarly, the two blanks in the innies must contain, collectively, 3 and 6.

This takes us to step 2 (next picture).

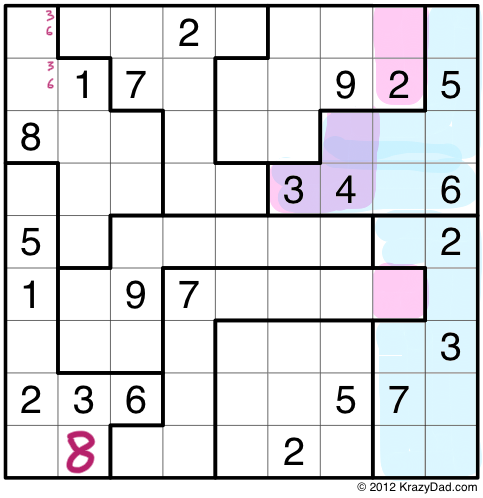
Here we have another case of innies and outies. In this case it involves two jigsaw pieces, which overlap with the two columns on the right. The Law of Leftovers can work with any number of puzzle pieces, and any number of rows/columns, as long as the number of pieces, and the number of columns are the same. Once again, the outies on the left, in purple, must be identical to the innies, in pink.

This means the one blank cell in the outies, must be 2, and the two blanks in the innies must be, collectively, 3 and 4. This brings us to step 3, shown below.

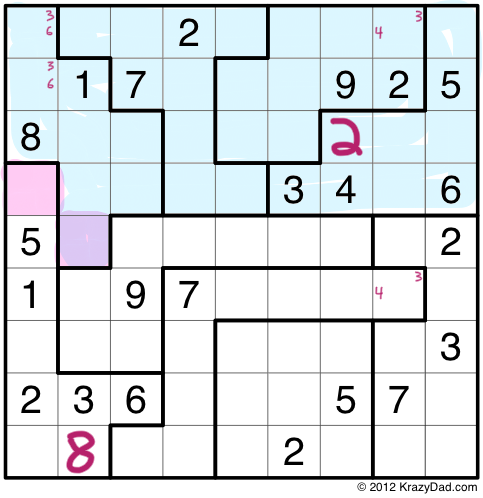
As I already mentioned, you can use the Law of Leftovers with any number of rows or columns, as long as the number of pieces you are overlapping is the same. Here I am overlapping 4 puzzle pieces with the top 4 rows. You’ll see that there is one outie, in purple, and one innie, in pink.

At this point, I don’t know what those two numbers are, but I know that they must be the same. This means that any constraints that apply to one cell must also apply to the other cell. Since I know that the innie, in the first column, can’t contain the numbers 1,2,3,4,5,6 or 8, I know that the outie also can’t contain those numbers. Thus I can narrow both cells down to the choices 7 and 9.

When solving these puzzles, I sometimes find it useful to leave known identical cells colored with the same color, which I’ll do here.

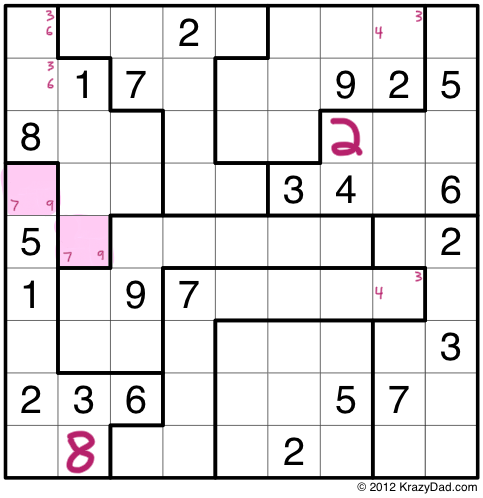
I’ll end the tutorial here, and give you a chance to find more outies and innies on your own.

I *do* want to mention that lately I’ve been doing these puzzles on an iPad, using the application UPAD. There are a few advantages to this method.

1) I get as many colored pencils and colored highlighters as I like, which is useful for jigsaw strategy,
as well as other advanced strategy.
2) If I make mistakes, I can erase/undo the colored markings easily. I can switch colors and do a few “what if” markings, then hit undo until I get back to the original color.
3) I can draw on each page of my books, and it leaves the drawings on each page intact.
4) No wasted paper/ink.
5) It still feels a lot like using pencil and paper, which I love – especially when I use a stylus.

Happy puzzling!

This entry was posted on Friday, September 7th, 2012 at 1:00 am and is filed under Puzzles. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.